4. Der Einfluss der Temperaturstrahlung auf ein Gebäude
1. Führt eine geometrische Wärmebrücke zu einem höheren Wärmestrom
2. Die Einflussnahme der Wärmekonvektion auf die
Oberflächentemperatur
3. Warum ist eine Erhöhung der Oberflächentemperatur im Eckbereich erforderlich?
Wie bereits genannt, kann Wärme durch Konvektion und durch Strahlung übertragen werden. Für die Übertragung der Wärmeenergie bei Strahlung ist kein Stoff als Träger erforderlich. So wie es zum Beispiel bei der Übertragung der Wärmeenergie von der Sonne auf die Erde erfolgt, der Zwischenraum ist praktisch stofffrei. Die Wärmestrahlung hängt von der jeweiligen Temperatur des strahlenden Körpers ab.
Dabei kann der Körper einen gasförmigen, flüssigen oder festen Aggregatzustand haben. Von der Oberfläche des Körpers werden aus innere Energie entstehende elektromagnetische Wellen geradlinig mit Lichtgeschwindigkeit ausgesendet (emittiert). Die Temperaturstrahlung umfasst den Wellenlängenbereich 0,8 bis 800 µm, wobei der Hauptanteil der ausgestrahlten Wärmeenergie im Bereich um 0,8 bis 10 µm liegt. (Sichtbares Licht für das menschliche Auge 0,4 bis 0,8 µm.)
Trifft
Temperaturstrahlung auf einen Körper,
so gibt es je nach Eigenschaft des Körpers verschieden
Möglichkeiten:
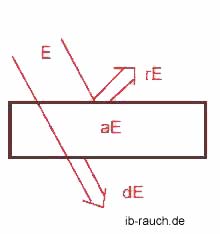
1. Der Körper kann die auftreffende Strahlung absorbieren.
2. Der Körper kann die auftreffende Strahlung reflektieren.
3. Der Körper kann die
Strahlung unverändert hindurchlassen.
Im Allgemeinen können alle drei Fälle gleichzeitig auftreten. Für die auftreffende Bestrahlungsstärke Ε (in W/m2) gilt:
Ε
= aΕ +rΕ + dΕ
1 = a + r + d
worin
aΕ absorbierte Teil,
rΕ reflektierte Teil,
dΕ durchgelassene Teil
Es bedeutet
a = Absorptionskoeffizient; r = Reflexionskoeffizient;
d = Durchlasskoeffizient.
Die in einem Körper
absorbierte Strahlung wird in innere
Energie zurück verwandelt. Das geschieht bei den meisten
festen und flüssigen
Körpern in einer sehr dünnen Randschicht. Zum
Beispiel bei elektrisch leitenden
Körpern schon in einer Tiefe von 0,001 mm und bei Nichtleitern
bis 1 mm.
Schwarze Körper haben a = 1.
Die Reflexion von Wärmestrahlung kann spiegelnd (bei blanken,
glatten
Oberflächen, Einfallswinkel gleich Ausfallswinkel) oder diffus
(matte
Oberflächen) erfolgen. Weiße Körper haben r
= 1.
Die Bezeichnung schwarzer oder weißer Körper
hängt vom Verhalten bei
Wärmestrahlung ab und darf nicht mit dem Aussehen verwechselt
werden. Für die
Wärmestrahlung nahezu schwarzer Körper sind zum
Beispiel Raureif (a =0,98), Ruß
(a=0,95) oder weiße Emaille (a=0,91). Weiße
Körper sind polierte Gold- oder
Kupferoberflächen mit a=0,02 bis 0,03. [6]
Bisher gibt es keine experimentellen Ergebnisse, wo die Strahlungsintensitäten von Festkörpern, Flüssigkeiten und Gasen bilanziert wird. Also mit welcher Intensitäten die Strahlungen aufgenommen und im IR-Bereich wieder abgestrahlt werden. In einem Gebäude liegen instationäre Bedingungen sowohl an der Gebäudehülle aber auch beim Strahlungskörper vor. Dieses thermodynamische System ist äußerst kompliziert. In der Verfahrenstechnik lässt sich der Strahlungsaustausch zwischen zwei parallelen ebnen Flächen oder einem Körper und seiner Umhüllung auf der Grundlage des Stefan-Boltzmannschen Gesetzes berechnen. Nach entsprechender Ableitung erhält man die Berechnungsgleichung für die Wärmestromdichte infolge Strahlung:
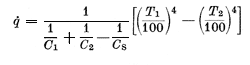
C1 Strahlungskoeffizient des wärmeren
Körpers
C2 Strahlungskoeffizient des weniger warmen Körpers
T Temperatur
q Wärmestromdichte
Bei der Temperaturstrahlung spielt die Temperatur der Raumluft keine Rolle. Sie dient nicht wie bei der Konvektion als Wärmträger. Die gleichmäßige Erwärmung der gesamten Wandoberfläche einschließlich der Gegenstände führt zu einer höheren Temperatur als die der Raumluft. Nicht nur, dass die Raumtemperatur bei gleicher Behaglichkeit niedriger sein kann, 1 K entspricht ca. 5% Heizenergie, ist die relative Luftfeuchte an der Wandoberfläche kleiner als in der Raumluft.
Der Strahlungsaustausch zwischen eingeschlossener und umschließender Fläche erfolgt in einem geschlossen Raum, sodass keine Strahlung den Raum verlässt. Hier wird dann auch der Größenunterschied zwischen den einzelnen Flächen berücksichtigt. Einmal der Wärmestrom von einem Strahlungsheizkörper an die Innenflächen des Raumes und der Wärmestrom von den Innenbauteilen zur Außenwand, wenn zum Beispiel die Heizung abgeschaltet ist. Die Berechnung erfolgt nach der Formel
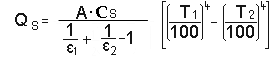
QS =Wärmestrom (neues Symbol Φ)
e = Emissionsverhältnis
A = Fläche
T = Temperatur in K
Cs = Strahlungskoeffizient in W/m²K4
Beispiel: Wärmestrom durch Wärmestrahlung am Beispiel
in einem
Wohnraum
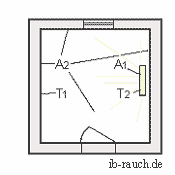 In
einem Zimmer mit der
Größe 3,5 x 4,5 und einer Höhe von 2,6 m
mit Raufasertapete und Holzfußboden
befindet sich eine Strahlungsheizung mit der Größe
von 2 m2 und einer Temperatur
von 50ºC. Die durchschnittliche Oberflächentemperatur
aller Raumflächen soll
17ºC betragen. Die Fensterfläche und die Tür
sollen vernachlässigt werden, da
sich die ε-Werte annähernd gleich sind und mit dem
geringen Flächenanteil nur
unwesentlich das Ergebnis beeinflussen.
In
einem Zimmer mit der
Größe 3,5 x 4,5 und einer Höhe von 2,6 m
mit Raufasertapete und Holzfußboden
befindet sich eine Strahlungsheizung mit der Größe
von 2 m2 und einer Temperatur
von 50ºC. Die durchschnittliche Oberflächentemperatur
aller Raumflächen soll
17ºC betragen. Die Fensterfläche und die Tür
sollen vernachlässigt werden, da
sich die ε-Werte annähernd gleich sind und mit dem
geringen Flächenanteil nur
unwesentlich das Ergebnis beeinflussen.
Welcher Wärmestrom wird vom Heizkörper an die Decke, Wände und den Boden des Zimmers durch Strahlung übertragen?
Berechnung
Flächen:
Heizkörper A1 = 2 m2
Raumwand/Decke A2a = [(3,5 + 4,0)× 2] × 2,6 + 3,5 × 4,0 = 53 m2
Fußboden A2b = 3,5 × 4,0 = 14 m2
Raumfläche A2 = A2a + A2b = 67 m2 bzw. Verhältnis 79,1% + 20,9% = 100%
Emissionsverhältnisse:
für Heizfläche
ε = 0,925 (für Heizkörperlack) und εn = 0,95 (für glatte Oberfläche)
ε1 = 0,925 × 0,95 = 0,88
für Wandflächen
ε = 0,92 (für Papier) und εn = 0,95 (für glatte Oberfläche)
ε2a = 0,92 × 0,95 × 79,1/100 = 0,691
für Fußbodenflächen
ε = 0,935 (für Holz) und εn = 0,95 (für glatte Oberfläche)
ε2b = 0,935 × 0,95 × 20,9/100 = 0,186
ε2 = 0,691 + 0,186 = 0,877
Strahlungskoeffizient des schwarzen Strahlers Cs = 5,77 W/(m2K4)
[experimentell bestimmt, J.H. Lambert 1728 bis 1777, Physiker,
Mathematiker].
Heute verwendet man die theoretisch begründeten Stefan-Boltzmann
Konstante 5,67051(19) x 10-8 W/m2K4. (Die Berechnungsformel ist zur Vereinfachung so aufgestellt, dass sich
die 10-8 Potenz aufhebt.)
Der durch die Strahlung übertragene Wärmestrom ist der Differenz der 4. Potenz der absoluten Temperatur und der Fläche proportional. Die Emissionsverhältnisse der beteiligten Flächen gehen in das resultierende Emissionsverhältnis ein. Da sich die Fläche des Strahlers (Heizfläche) gegenüber der umhüllende Fläche A1 << A2 verhält, wird A1/A2 ~ 0 und das resultierende Emissionsverhältnis ist nur vom eingeschlossenen Körper (Heizfläche) abhängig.
Resultierendes Emissionsverhältnis
1 1
ε12 = --------------------------- = -------------------------------------------- = 0,876
1/ε1 + A1/A2(1/ε2 - 1) 1/0,88 + 2,0 m2/67 m2(1/0,877 - 1)
Wärmestrom von der Strahlenheizung:
Qs = A1ε12Cs [(T1/100)4 - (T2/100)4]
= 2,0 m2 x 0,876 x 5,67 W/m2K4 [(323 K/100)4 - (290/100)4]
= 379 W
bzw. 379 W/67 m2 = 5,7 W/m2Raumfläche
Der Wärmestrom vom Strahlungsheizkörper an die Innenflächen des Raumes liegt bei 385 W bzw. 5,7 W pro m2 Raumfläche.
Von jeder Körperoberfläche geht stets emittierte (eigene) und reflektierte (fremde) Strahlung aus. Das bedeutet bei diesem Beispiel, wenn die Temperatur der Oberfläche der Außenwand absinkt, so erfolgt nicht nur ein Wärmestrom vom Heizkörper, sondern auch von den anderen innen liegenden Wandoberflächen. Vorausgesetzt ihre Oberflächentemperatur ist höher, als die der Außenwand. Es ist also sehr sinnvoll, die innen liegenden Oberflächen aus massiven Wänden mit großem Wärmespeichervermögen (siehe Auskühlzeit der Baustoffe) herzustellen. Diese geben dann noch über eine lange Zeit Wärmestrahlung ab. Dies soll in der nachfolgenden vereinfachten Berechnung dargestellt werden.
Die Strahlenheizung des oben betrachten Raums wird abgeschaltet. Die Außenwand ist 10,4 m2 (4,0 m x 2,6 m) groß und soll eine Oberflächentemperatur von 15ºC haben. Die übrige Fläche von 56,5 m2 hat durchschnittlich eine Temperatur von 17,4ºC. Dies ergibt sich aus der Durchschnittstemperatur aller Flächen mit 17ºC. Für die Emissionsverhältnisse für die Wandflächen gelten die oben genannten Werte.
Resultierendes Emissionsverhältnis
1 1
ε12 = ------------------------------ = -------------------------------------------------- = 0,86
1/ε1 + A1/A2(1/ε2 - 1) 1/0,877 + 10,4 m2/56,4 m2(1/0,877 - 1)
Wärmestrom von den Innenbauteilen zur inneren Wandoberfläche der Außenwand:
Qs = A1ε12Cs [(T1/100)4 - (T2/100)4]
= 10,4 m2 × 0,86 × 5,67 W/m2K4 [(290,4 K/100)4 - (288/100)4]
= 117,6 W ~ 120 W
Die Wärmeübertragung erfolgt durch Wärmestrahlung und Wärmekonfektion, daher ist auch der innere Wärmeübergangskoeffizient durch Konvektion zu beachten.
Der Architekt Herr Konrad Fischer beschreibt in seinem Vortrag "Konservatorische Temperierung" im April 2006 im Schloss Veitshöchheim Holzvermorschungen in der Deckenkonstruktion sowie Schimmelbefall an den Papiertapeten im Obergeschoss als Ergebnis dauerhaft zu hoher Materialfeuchte durch Kondensataufnahme. Insgesamt konnte die Hüllflächentemperierung im Schloss Veitshöchheim die positive Wirkung der Wärmestrahlungs-Temperiertechnik im speicherfähigen Massivbau aus konservatorischer und energetischer Sicht praktisch belegt werden. [8]
Bei der Temperaturstrahlung liegt keine bzw. nur eine geringe Luftströmung vor. Damit wird der Wärmeübergangskoeffizient α klein, sodass der Wärmestrom durch die Außenwand die entscheidende Bewertungsgröße ist. Da im Eckbereich der Wandquerschnitt am größten ist, ist hier, wie bereits zum Anfang festgestellt wurde, auch der Wärmestrom gegenüber der übrigen Wandfläche kleiner, welche durch die Vergrößerung der gegenüberliegenden Außenfläche kompensiert wird. Dass ein Vieleck nicht zu einer Erhöhung des Wärmestroms führt, wurde rechnerisch nachgewiesen. Aus den genannten Sachverhalten lässt sich nicht zweifelsfrei ableiten, dass wegen der niedrigeren Oberflächentemperatur im Eckbereich auch ein höherer Wärmestrom vorliegt, der durch eine äußere Wärmedämmung zu beseitigen ist.
Wesentlich komplizierter ist die Berechnung des Wärmestroms an den Außenwänden bei einem Wohngebäude. Hier sind die Flächen, mit denen ein Strahlungsaustausch erfolgt, weder gleich groß und liegen zusätzlich schräg zueinander. einem Gebäude ist daher äußerst kompliziert.
Dipl. Ing.oec., Ing. Peter Rauch 10.10.2010
Ergänzung:
Messung der IR-Strahlungstemperatur an einem Satteldach
Energetische Messung der IR-Strahlungstemperatur an einer Halbkugel
Literatur:
[1] Meyer, G., Schiffner, E.: Übungen zur Technischen
Thermodynamik, VEB Fachbuchverlag Leipzig 1986 S.15
[2] Clausius, Rudolf; Die mechanische Wärmetheorie,
3. Aufl., Vieweg Braunschweig 1887 S. 25,
[3] Clausius, Rudolf; Die mechanische Wärmetheorie, 3. Aufl.,
Vieweg Braunschweig 1887 S. 81
[4] Günter Meyer, Erich Schiffner; Technische
Thermodynamik, 2. Aufl., 1983, Fachbuchverlag
Leipzig S. 365
[5] Günter Meyer, Erich Schiffner; Technische Thermodynamik,
2. Aufl., 1983, Fachbuchverlag Leipzig S. 208
[6] Günter Meyer, Erich Schiffner; Technische Thermodynamik,
2. Aufl., 1983, Fachbuchverlag Leipzig S. 220
[7] Günter Meyer, Erich Schiffner; Technische Thermodynamik,
2. Aufl., 1983, Fachbuchverlag Leipzig S. 247f
[8] Fischer, Konrad; Vortrag, Konservatorische
Temperierung Grundlagen, Planung, Ausführung,
Arbeitsgemeinschaft Deutscher Schlösserverwaltungen
[9] Rauch,
Peter; Wärmeleitfähigkeit ib-rauch.de/bauphysik/formel/warmleit.html
[10] Weinmann Kur; Handbuch Bautenschutz Bd. 2, Bauphysik und
Bauchemie, expert Verlag 1992, S. 56
[11]Günter Meyer, Erich Schiffner; Technische Thermodynamik,
2. Aufl., 1983, Fachbuchverlag Leipzig S. 368 Die Werte wurden aus den
Tafelwerten interpoliert.
[12]Jaroslav Rímal, Marcus Hermes; Die
energiesparende
Gebäudehülle, GFF 12/2006, S. 28ff
[13] Jaroslav Rímal, Marcus Hermes; Die energiesparende
Gebäudehülle, GFF 12/2006, S. 32
[14] Werner, Hanns; In Gösel, Karl; Schüle, Walter;
Künzel, Helmut; Schall, Wärme, Feuchte Grundlagen,
neue Erkenntnisse und Ausführungshinweise für den
Hochbau, 10.Aul., 1997, Bauverlag Wiesbaden/Berlin, S. 188
[16] Höherer Wohnwert durch Ziegelbauweisen,
bau-zeitung
52(1998)12 S. 43-45
[17] Königwinter, Peters; Wärmebrücken im
Mauerwerksbau beachten, Baumarkt 10/99 S. 10-15
[18] Schild, E.; Casselmann, H.F.; Dahmen, G. Pohlenz, R.; Bauphysik
-Planung und Anwendung, 4. Auflage, 1990 Vieweg Verlag Braunschweig
[19] Jaroslav R(ímal, Marcus Hermes; Die energiesparende
Gebäudehülle, GFF 12/2006, S. 28ff
[20] Wetzell, Otto W.; Wendehorst, Bautechnische
Zahlentafeln 26. Aufl. ,BG. Teubner Stuttgart Beuth Verlag Berlin und
Köln 1994, S. 131
[21] Reuter, Gunhild; Schimmelpilz in der Wohnung 2006
Dashöfer Holding Ltd., Zypern & Verlag
Dashöfer GmbH, Hamburg, S. 2
[22]Friedrich, Horst, Arndt, Claus; Bautechnischer Wärme- und
Feuchtigkeitsschutz 1989, Bauverlag S.223
[23]Oswald, R.; Wärmebrücken in
Außenwänden, Vortag Altbausanierung am 11.1.1993 an
der IHK Leipzig
[24]Werner, Hanns; In Gösel, Karl; Schüle, Walter;
Künzel, Helmut; Schall, Wärme, Feuchte Grundlagen,
neue Erkenntnisse und Ausführungshinweise für den
Hochbau, 10.Aul., 1997, Bauverlag Wiesbaden/Berlin, S. 187
[25] Jaroslav R(ímal, Marcus Hermes; Die energiesparende
Gebäudehülle, GFF 12/2006, S. 31
[26] DIN Deutsches Institut für Normung e.V.
Wärmebrücken im Hochbau. Allgemeine
Berechnungsverfahren. Deutsche Fassung EN ISO 10211-1:1995. Ausgabe
November 1995; Beuth Verlag GmbH, Berlin.
[27] Jaroslav Rímal, Marcus Hermes; Die energiesparende
Gebäudehülle, GFF 12/2006 S. 32
14.10.2007
© Altbausanierung | Bauideen | Blog | Sanierungskosten | Wohnen | Impressum | AGB/Datenschutzerklärung | 7/2018 ![]()







